加减运算电路实验
实验原理
加减运算
加法运算是最基本的算术运算,其运算速度对计算机的运行速度有着重要影响。4位的加法器可以用4个全加器级联构成,由于存在进位链的传递延时,运算速度随着精度的提高(位数增加)而降低。所以实际的并行加法器并不会采用全加器级联的方法,而是采用先行进位加法器。在硬件描述语言中,可以直接用“+”号描述并行加法器,综合工具会自动使用库中的先行进位加法器,而不用设计者描述先行进位的实现细节。
计算机中的带符号整数通常采用补码表示,因为补码可以连同符号位一起参加运算,这样就可以用二进制加法器完成补码加法运算,并且补码的减法也可以转换为加法,只需要在加法器的基础上增加求补电路就可以实现减法,而不用为减法设计专门的电路。
图 1是一种基本的加减运算电路,用M控制异或门实现求补运算,当M=0时做加法运算,M=1时做减法运算。该电路还产生S、Z、O、C四个运算结果的特征标志位(也称作条件码condition code),通常用于数值大小的比较判断。
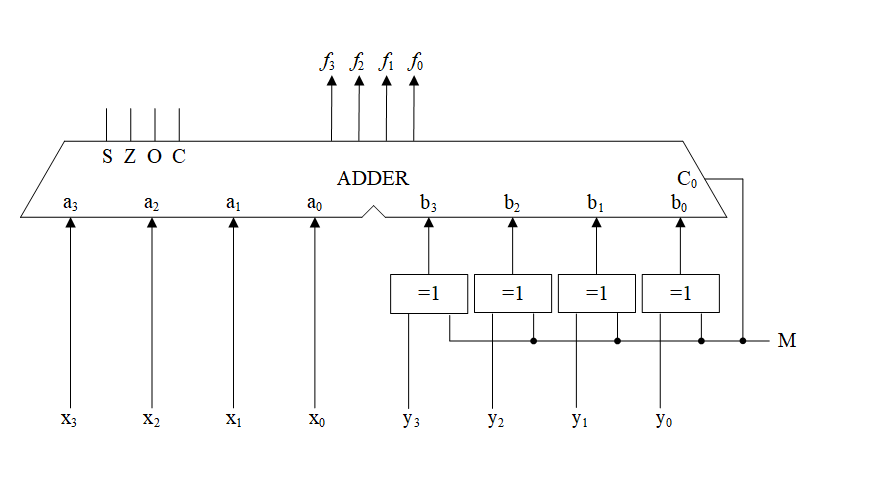
比较运算
在计算机软件程序设计中,常常需要比较两个变量的数值大小。实现两个数大小比较的最直接的做法就是将这两个数相减,根据减法的结果判断两者的大小。例如,若X<Y,则X-Y的结果一定为负,因此依据符号标志就可以判断;但是若运算结果溢出,则恰恰相反。表 1给出了两个带符号数依据减法运算结果的标志位比较大小的判断条件。而两个无符号数的相减,则可依据是否有借位来判断两个数的大小。表 2给出了无符号数比较大小的判断条件。
| 大小关系 | 判定条件 |
|---|---|
X>Y |
OF⊕SF=0 且ZF=0 |
X≥Y |
OF⊕SF =0 |
X=Y |
ZF=1 |
X≠Y |
ZF=0 |
X<Y |
OF⊕SF =1 |
X≤Y |
OF⊕SF =1 或ZF=1 |
| 大小关系 | 判定条件 |
|---|---|
X>Y |
CF=0 且ZF=0 |
X≥Y |
CF=0 |
X=Y |
ZF=1 |
X≠Y |
ZF=0 |
X<Y |
CF=1 |
X≤Y |
CF=1 或ZF=1 |
上述利用标志位进行数值比较的方法可以看成是加减电路的附带功能,没有增加多少硬件成本;但是比较的速度却不够快,因为经过了加减电路、标志位生成,再根据标志位产生比较结果,电路的传输延时较长。
为了提高比较速度,可以使用专用的数值比较电路。就像先行进位已经成为并行加法器的基本模块,比较器也是一种基本的运算模块,使用硬件描述语言的比较运算符,综合工具会自动生成比较器模块。
实验内容和要求
理解参考设计
实验材料中给出了图 1电路的HDL设计,阅读理解代码,通过实验验证电路功能,并回答以下问题。
(1)该电路是否既可以进行无符号数的加减运算,也可以进行带符号数的加减运算?
(2)溢出标志的生成代码如下,如果不用B的符号位而是Y的符号位,会有什么问题?
assign overflow = (~A[3]) & ~B[3] & F[3] | (A[3]) & B[3] & ~F[3] ;
(3)进位标志的生成代码如下,为什么要考虑M=0和M=1两种情况?
assign carryOut = (M==1'b0) ? result[4] : ~result[4];
(4)如何使用该电路判断两个数的大小?
设计任务:加减和比较运算电路
按照图 2原理设计运算电路,其核心电路和参考设计一样,都是加法器ADDER,完成F=A+B+C0的加法运算;和图 1相比,它的B输入端电路和C0输入端不同。B输入端电路包含与或门构成的二选一多路器(前面的“三态门与多路器实验”做过),该电路的特点是可以通过M0和M1的控制在B输入端产生“全0”和“全1”数据(与Y输入数据无关),用于一些特殊的功能,例如将X输入端的数据传送到F输出端。
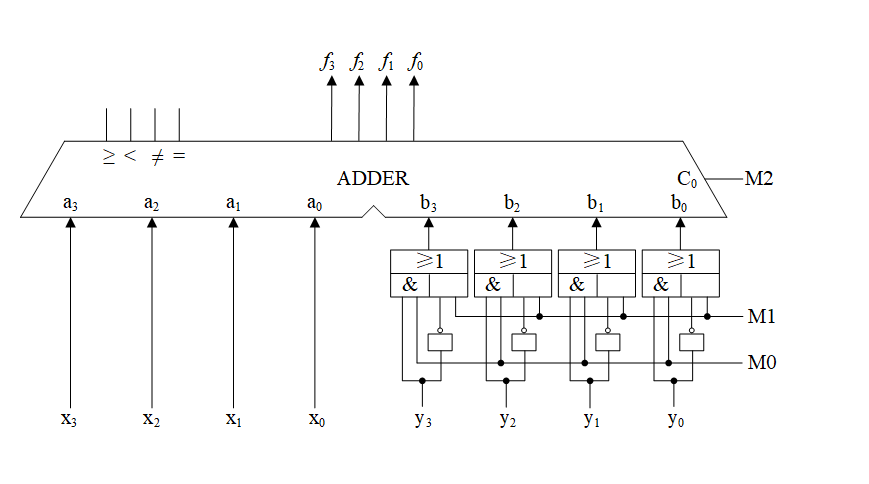
| M2 | M1 | M0 | 运算 | 功能描述 |
|---|---|---|---|---|
0 |
0 |
0 |
F=X |
传送X(MOVX) |
0 |
0 |
1 |
||
0 |
1 |
1 |
||
1 |
0 |
0 |
||
1 |
1 |
0 |